This post was written in collaboration with Almog Simchon (@almogsi) and Shachar Hochman (@HochmanShachar). Go follow them.
The fictional simplicity of Generalized Linear Models
Who doesn’t love GLMs? The ingenious idea of taking a response level variable (e.g. binary or count) and getting some link function magic to treat it as if it was our long-time friend, linear regression.
In the last few days, a preprint by McCabe et al. popped up in our twitter feed (recommended reading!) and re-focused our attention on the problem with interpreting effects and interactions within the GLM framework. McCabe et al. state in the abstract that:
“To date, typical practice in evaluating interaction effects in GLMs extends directly from linear approaches, in which the product term coefficient between variables of interest are used to provide evidence of an interaction effect. However, unlike linear models, interaction effects in GLMs are not equal to product terms between predictor variables and are instead a function of all predictors of a model.”
The what-now?
When fitting a GLM we think of the response level (the binary outcome or the counts that interest us), however, the model is fit (and often all statistical inferences are done) on the latent level - in the realm of the link function.
For interactions (but as you will see soon, not only), it means that when we test the effect of X1 at different levels of X2, we’re testing these effects on the latent (e.g., logistic) level, which might not represent these effects on the response level!
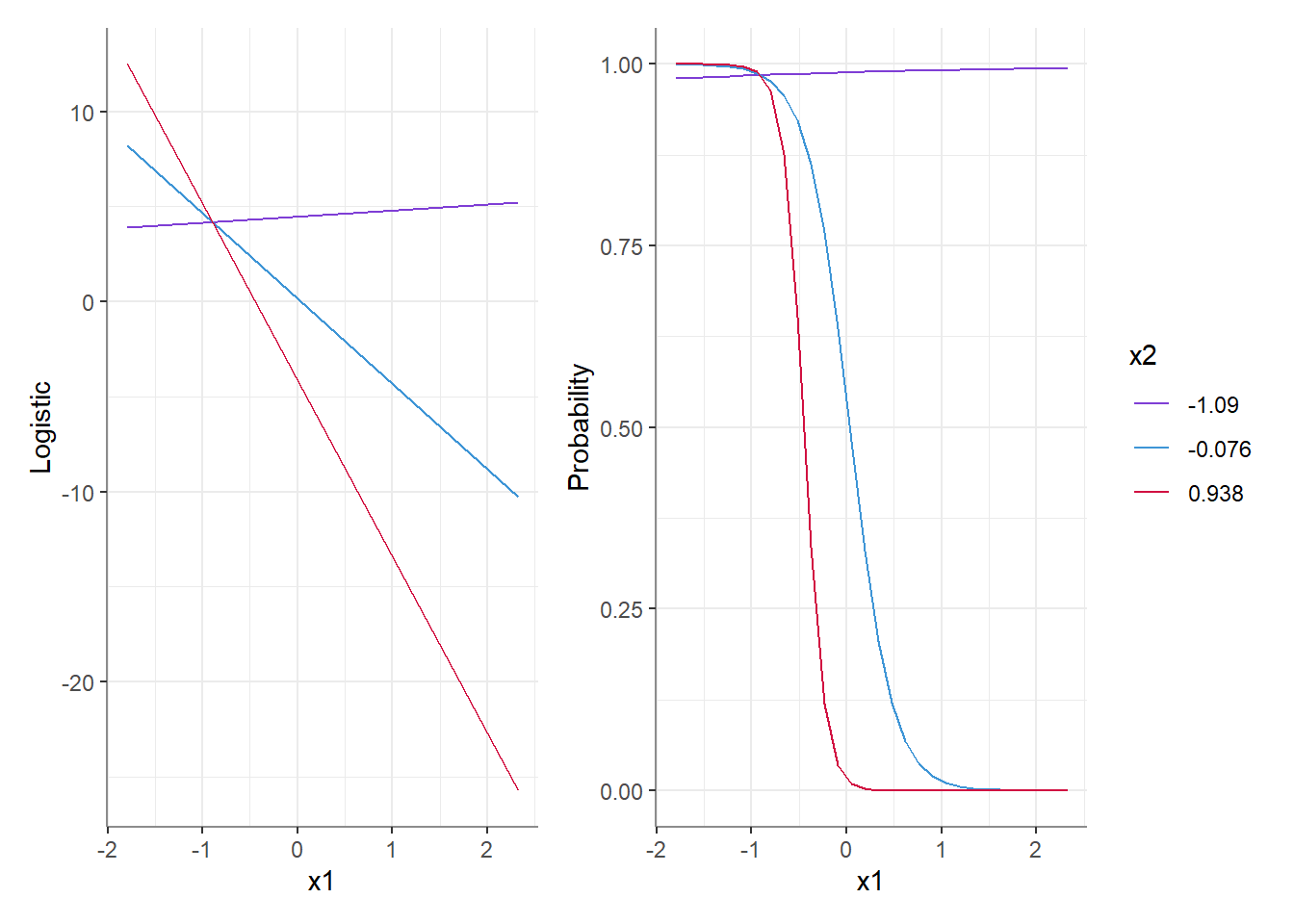
For example, both plots above represent corresponding predictions from the same interaction-model - on the left we have those predictions on the latent level, and on the right these have been transformed back to the response level (the probability). We can see that at the latent level, the effect of X1 on y is very different at all levels of X2, but at the response level these differences can shrink or possibly disappear (e.g., red vs. blue lines), or get larger (red and blue vs. purple line).
This is true regardless of whether or not an interaction was included in the model! And in fact, even main effects on the latent level do not always correspond to the response level the way we would have intuitively imagined.
What follows are 3 methods for testing interactions in GLMs, using emmeans. Again, we highly recommend reading McCabe et al.’s original paper.
Let’s load up some packages:
library(emmeans) # 1.8.4.1
library(magrittr) # 2.0.3 The Model
The model used here is a logistic regression model, using data adapted from McCabe et al., except we’re using a binomial outcome (see code for data generation at the end of the post):
y <- plogis(xb) < 0.01
model <- glm(y ~ x1 * female + x2,
data = df,
family = "binomial")Using emmeans for estimation / testing
If you’re not yet familiar with emmeans, it is a package for estimating, testing, and plotting marginal and conditional means / effects from a variety of linear models, including GLMs.
So let’s answer the question:
Does the effect of sex (
female) differ as a function ofx1, and how does this interaction differ as a function ofx2.
We will use the pick-a-point method for both continuous variables:
- For
x1: -1, +1 - For
x2: mean +- sd
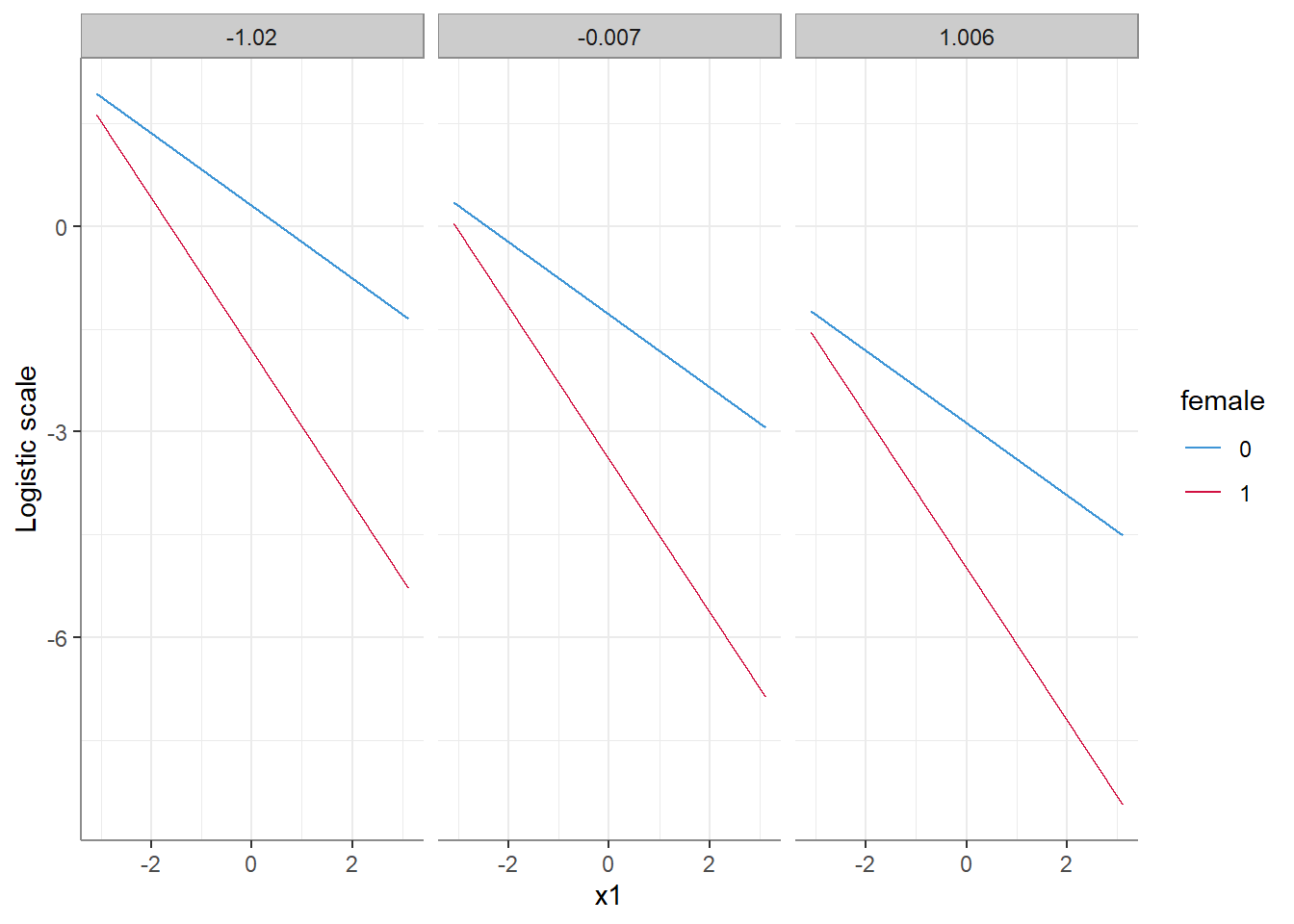
1. On the latent level
emmeans(model, ~ x1 + female + x2,
at = list(x1 = c(-1, 1)),
cov.reduce = list(x2 = mean_sd)) %>%
contrast(interaction = c("pairwise", "pairwise"),
by = "x2")x2 = -1.020:
x1_pairwise female_pairwise estimate SE df z.ratio p.value
(-1) - 1 0 - 1 -1.17 0.497 Inf -2.350 0.0188
x2 = -0.007:
x1_pairwise female_pairwise estimate SE df z.ratio p.value
(-1) - 1 0 - 1 -1.17 0.497 Inf -2.350 0.0188
x2 = 1.006:
x1_pairwise female_pairwise estimate SE df z.ratio p.value
(-1) - 1 0 - 1 -1.17 0.497 Inf -2.350 0.0188
Results are given on the log odds ratio (not the response) scale. It seems that on the latent level the (estimated) difference of differences (the interaction) between female and x1 is unaffected by which level of x2 they are conditioned on. This makes sense - we did not model a 3-way interaction, so why should it? Everything is acting as expected.
Or is it? Well, that depends…
2. On the response level (the delta method)
We can also try and answer the same question on the response level using the delta method (baked into emmeans). Here we have two options for defining an “effect”:
- An effect is a difference in probabilities.
- An effect is a ratio of probabilities.
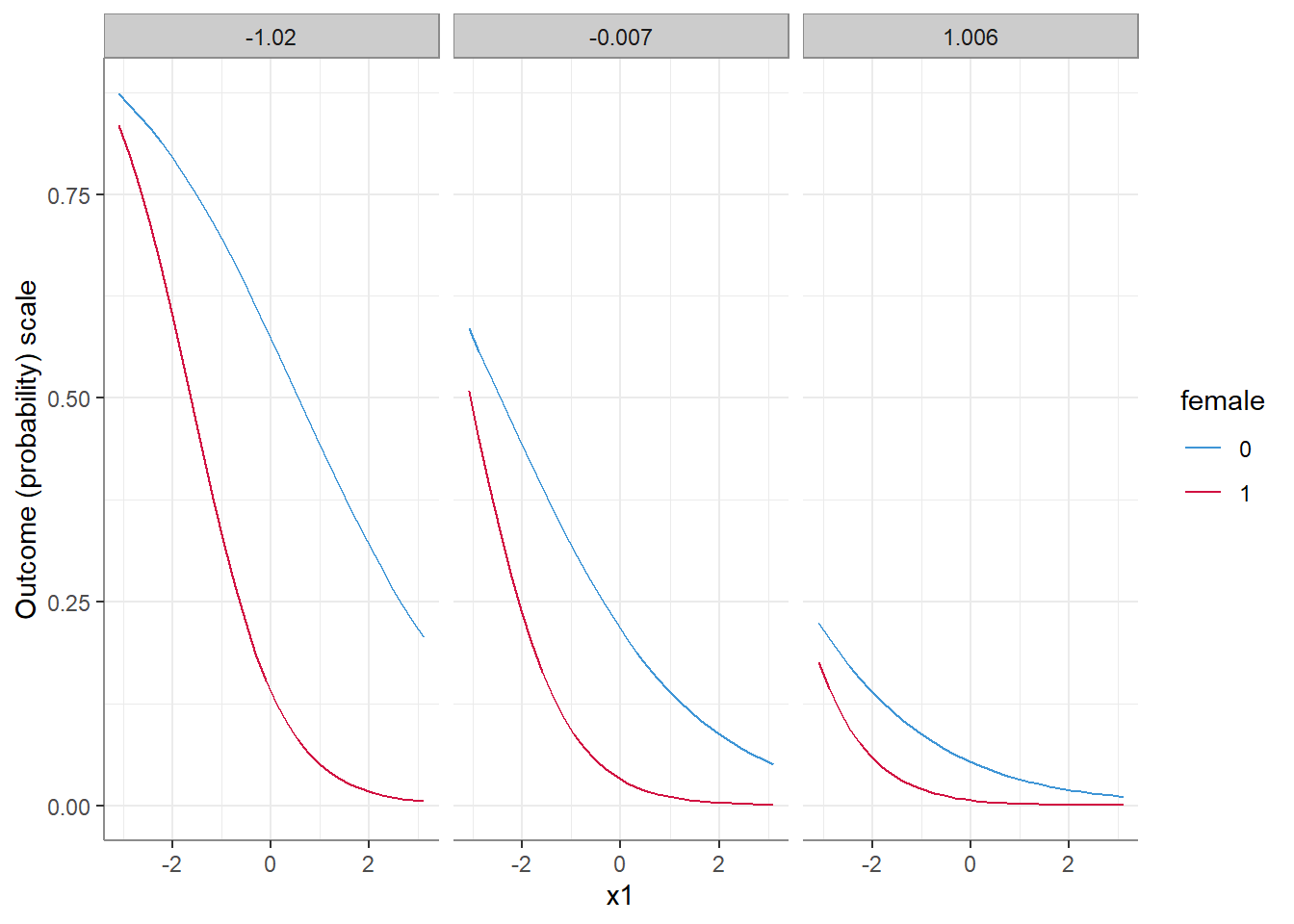
2.1. Differences in probabilities
For this, we just need to add trans = "response" in the call to emmeans():
emmeans(model, ~ x1 + female + x2,
at = list(x1 = c(-1, 1)),
cov.reduce = list(x2 = mean_sd),
trans = "response") %>%
contrast(interaction = c("pairwise", "pairwise"),
by = "x2")x2 = -1.020:
x1_pairwise female_pairwise estimate SE df z.ratio p.value
(-1) - 1 0 - 1 -0.0265 0.0787 Inf -0.336 0.7365
x2 = -0.007:
x1_pairwise female_pairwise estimate SE df z.ratio p.value
(-1) - 1 0 - 1 0.0976 0.0470 Inf 2.075 0.0380
x2 = 1.006:
x1_pairwise female_pairwise estimate SE df z.ratio p.value
(-1) - 1 0 - 1 0.0371 0.0163 Inf 2.279 0.0227# Difference of differences when x2 = -1.02
(0.69457 - 0.44178) - (0.32986 - 0.05059)[1] -0.02648It seems that on the response level, we get different results than on the latent level. And not only that, but even though the model did not include a 3-way interaction, the 2-way female:x1 interaction is conditional on the level of x2 - changing in size as a function of x2, and is not significant in low levels of x2!
2.2. Ratios of probabilities
(Also called risk ratios.)
For this, we just need to add trans = "log" and type = "response" in the call to emmeans():
emmeans(model, ~ x1 + female + x2,
at = list(x1 = c(-1, 1)),
cov.reduce = list(x2 = mean_sd),
trans = "log",
type = "response") %>%
contrast(interaction = c("pairwise", "pairwise"),
by = "x2")x2 = -1.02:
x1_pairwise female_pairwise ratio SE df null z.ratio p.value
(-1) / 1 0 / 1 0.241 0.097 Inf 1 -3.534 0.0004
x2 = -0.007:
x1_pairwise female_pairwise ratio SE df null z.ratio p.value
(-1) / 1 0 / 1 0.268 0.124 Inf 1 -2.856 0.0043
x2 = 1.006:
x1_pairwise female_pairwise ratio SE df null z.ratio p.value
(-1) / 1 0 / 1 0.299 0.146 Inf 1 -2.480 0.0131
Tests are performed on the log scale # Ratio of ratios when x2 = -1.02
(0.69457 / 0.44178) / (0.32986 / 0.05059)[1] 0.2411265It seems that even on the response level, different delta methods produce different results!1 Although we maintain the finding that the size of the 2-way female:x1 interaction is conditional on the level of x2, here it decreases as a function of x2 (but is significant across all (tested) values of x2)!
(Note: as we are interested in the slope of x1, we could have used emtrends instead of emmeans. See code at the end of the post for what that would look like.)
Not just a problem with interactions…
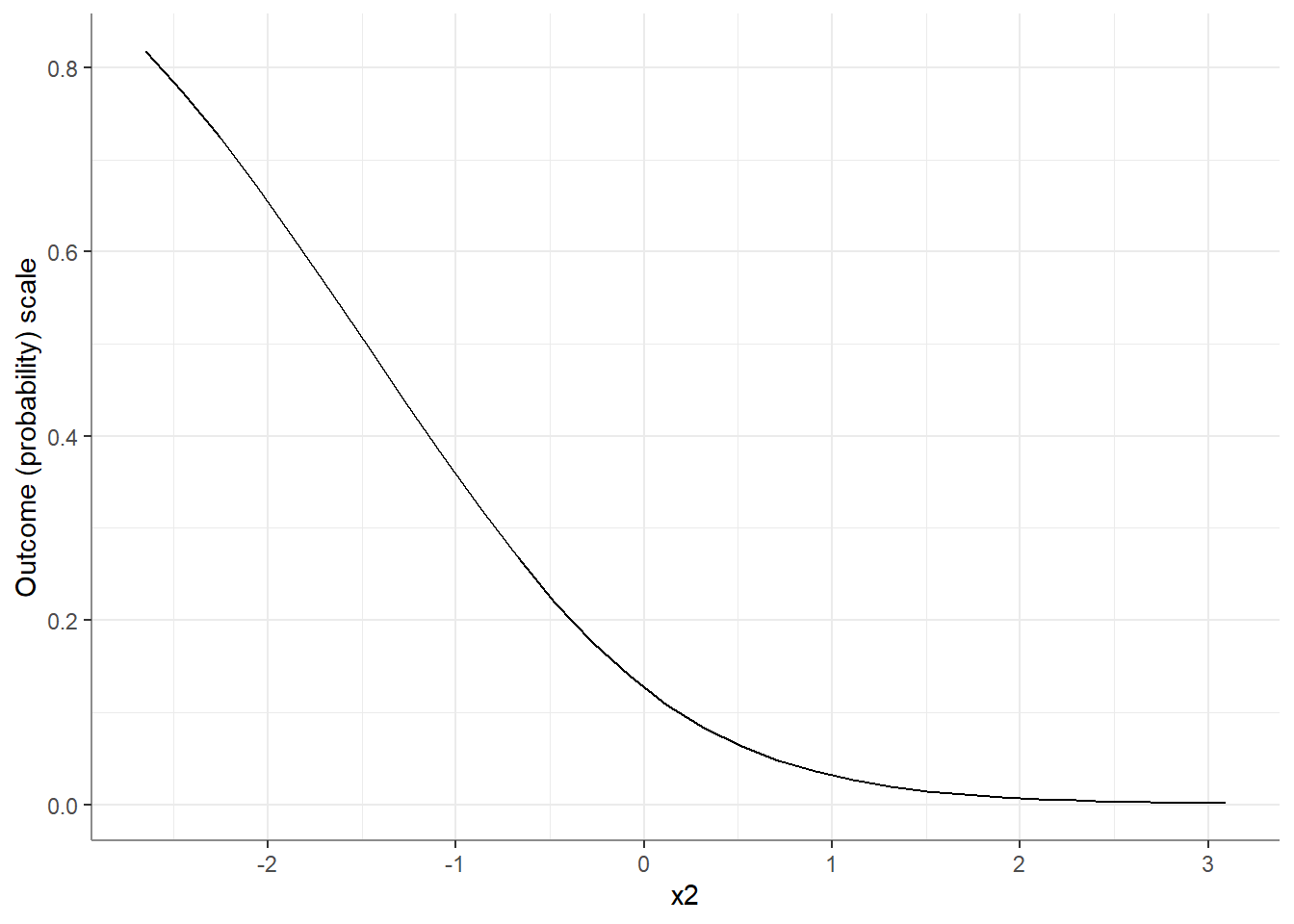
As stated above, this is not only an issue of interactions. For example, when looking at the response level, the effect of x2 is itself conditional on the value of x2!
emmeans(model, ~ x2,
cov.reduce = list(x2 = mean_sd),
trans = "response") %>%
contrast(method = "consec") contrast estimate SE df z.ratio p.value
(x2-0.007) - (x2-1.02) -0.2361 0.02190 Inf -10.782 <.0001
x21.006 - (x2-0.007) -0.0965 0.00825 Inf -11.695 <.0001
Results are averaged over the levels of: female
P value adjustment: mvt method for 2 tests Note how the estimated effect of x2 is smaller for larger values of x2!
Conclusion
The growing popularity of GLMs (and GLMMs) in social research seems to come with another source of researcher degrees of freedom (and we all know how well that works for us)…
What should you do?

Honestly, we don’t know. Some of us feel that since the response variable is our variable of interest, that’s what we should be focusing on; some of us feel that with no common practice, we should stick to the latent level; some of us are agnostic (that covers all of us). We can’t recommend one approach, but we do think that when fitting and working with GLMs, this is a consideration one has to face.2 Good luck!

Make the data and model
set.seed(1678)
b0 <- -3.8 # Intercept
b1 <- .35 # X1 Effect
b2 <- .9 # X2 Effect
b3 <- 1.1 # Sex covariate effect
b13 <- .2 # product term coefficient
n <- 1000 # Sample Size
mu <- rep(0, 2) # Specify means
# Specify covariance matrix
S <- matrix(c(1, .5, .5, 1),
nrow = 2, ncol = 2)
sigma <- 1 # Level 1 error
# simulates our continuous predictors from a multivariate
# normal distribution
rawvars <- MASS::mvrnorm(n = n, mu = mu, Sigma = S)
cat <- rbinom(n = n, 1, .5)
id <- seq(1:n)
eij <- rep(rnorm(id, 0, sigma))
xb <- (b0) +
(b1) * (rawvars[, 1]) +
(b2) * (rawvars[, 2]) +
(b3) * cat +
b13 * cat * (rawvars[, 1]) +
eij
df <- data.frame(x1 = rawvars[, 1],
x2 = rawvars[, 2],
female = cat)
y <- plogis(xb) < 0.01
model <- glm(y ~ x1 * female + x2,
data = df,
family = "binomial")Using emtrends
Note that the inferential results (\(z\) and \(p\) values) are similar (though not identical) to those obtained using emmeans.
# log(odds)
emtrends(model, ~ female + x2, "x1",
cov.reduce = list(x2 = mean_sd)) %>%
contrast(method = "pairwise", by = "x2")x2 = -1.020:
contrast estimate SE df z.ratio p.value
female0 - female1 0.584 0.248 Inf 2.350 0.0188
x2 = -0.007:
contrast estimate SE df z.ratio p.value
female0 - female1 0.584 0.248 Inf 2.350 0.0188
x2 = 1.006:
contrast estimate SE df z.ratio p.value
female0 - female1 0.584 0.248 Inf 2.350 0.0188# diffs
emtrends(model, ~ female + x2, "x1",
cov.reduce = list(x2 = mean_sd),
trans = "response") %>%
contrast(method = "pairwise", by = "x2")x2 = -1.020:
contrast estimate SE df z.ratio p.value
female0 - female1 0.0107 0.04117 Inf 0.259 0.7957
x2 = -0.007:
contrast estimate SE df z.ratio p.value
female0 - female1 -0.0542 0.02399 Inf -2.259 0.0239
x2 = 1.006:
contrast estimate SE df z.ratio p.value
female0 - female1 -0.0195 0.00793 Inf -2.457 0.0140# ratios
emtrends(model, ~ female + x2, "x1",
cov.reduce = list(x2 = mean_sd),
trans = "log", type = "response") %>%
contrast(method = "pairwise", by = "x2")x2 = -1.020:
contrast estimate SE df z.ratio p.value
female0 - female1 0.727 0.207 Inf 3.509 0.0004
x2 = -0.007:
contrast estimate SE df z.ratio p.value
female0 - female1 0.663 0.233 Inf 2.848 0.0044
x2 = 1.006:
contrast estimate SE df z.ratio p.value
female0 - female1 0.605 0.244 Inf 2.476 0.0133